Skip to main content

Not Just Calculus: First-Year Introduction to Upper-Level Mathematics

David W. Lyons

Section 1.5 Problems

Subsection 1.5.1 Linear and Exponential Growth

Exercises Exercises

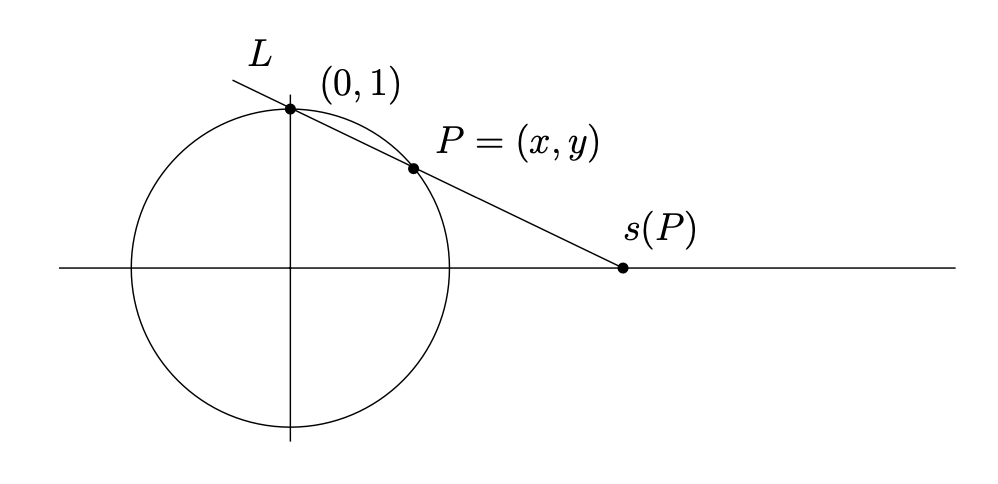
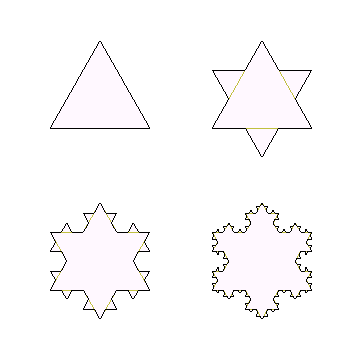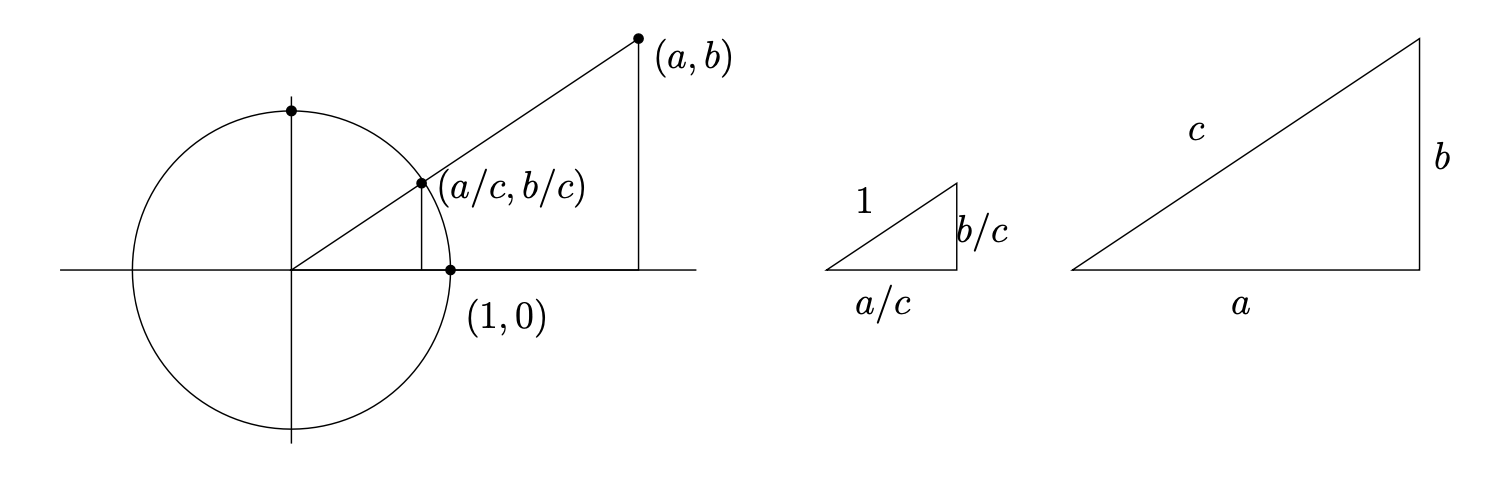1.
Consider the following true life situation.
"I want to rent this room for the month of July," he said. The clerk wheezed. He peered through the narrow slits of his bloodshot eyes, glaring through the murk of the humid dusty darkness of the fleabag lobby, and said, "for you—a deal." "How much?" said the big guy, sweat trickling down his face, staining the collar of his dingy shirt which didn’t appear to have been washed in weeks. Noticing the telltale bulge of a revolver under the stranger’s dirt stained jacket, the clerk replied, "First day—one cent. Second day—two cents. Third day—four. Every day it doubles." The stranger’s face drew into a knot as he scrutinized the greasy poker faced clerk. He said, "That’s nothin’. What’s the hitch?"
  1. How much would the stranger pay on July 31st?
  2. What would the bill be for the month of July?
2.
Gumby and Pokey decide to go on a diet together. Gumby and Pokey both weigh \(10\) ounces. Starting their diets on the same day, Gumby loses \(1/10\) of an ounce each day, while Pokey loses half his body weight each day.
  1. Who wins the race to the body weight of 1 ounce?
  2. Explain how you know, without calculating, that Gumby will win the race to zero body weight.
  3. How much of Pokey is left when Gumby vanishes?
3. Zeno’s Paradox.
The Greek philosopher Zeno (ca. 450BC) considered the following motion problem. A rabbit and a turtle agree to run a race. Displaying good sportsmanship, the rabbit, who can run faster, gives the turtle a head start. Zeno argued that the rabbit will never catch the turtle, as follows. To catch the turtle, the rabbit must first travel from the starting point to the turtle’s starting point. During this time, the turtle will advance. Let’s call the turtle’s new location point 2. Now the rabbit must travel to point 2, but during that time, the turtle advances to point 3. And so on. This process defines an infinite sequence of distinct points. Traveling from each one to the next requires a positive amount of time. Since an infinite sum of positive numbers must be infinite, Zeno concludes that the rabbit will never catch the turtle. Of course, Zeno knew there must be some flaw in this argument, but was unable to resolve the paradox satisfactorily.
Analyze Zeno’s paradox under the following assumptions: the rabbit travels at a constant speed of 5 feet per second; the turtle travels at a constant speed of 2 feet per second; and the head start distance is 10 feet. Place coordinates on the race track with the rabbit beginning at 0 and the turtle beginning at 10, with both running in the positive direction.
  1. Using high school algebra and the formula
    \begin{equation*} (\text{distance}) = (\text{rate})(\text{time}) \end{equation*}
    find the location where the rabbit catches the turtle, and the time elapsed from the beginning of the race to the point where the rabbit catches the turtle.
  2. Find the sequence of distances traveled by the rabbit from the rabbit’s starting point to the turtle’s starting point, from there to point 2, from point 2 to point 3, etc.
  3. Find the sequence of times that elapse while the rabbit traveled the distance intervals in the previous part.
  4. Use the theory of geometric sequences to resolve Zeno’s paradox by reconciling your findings in the previous steps of this problem.
4.
The following problem is a modern version of Zeno’s paradox. It is taken from an article by George Andrews in the January 1998 issue of the American Mathematical Monthly, Vol. 105 No. 1 and is attributed to a Prof. Sleator.
Two trees are one mile apart. A drib flies from one tree to the other and back, making the first trip at 10 miles per hour, the return at 20 miles per hour, the next at 40 and so on, each successive mile at twice the speed of the preceding.
  1. Write the first five terms of the sequence of velocities for trip numbers 1, 2, 3, etc. Write an explicit formula for this sequence.
  2. Write the first five terms of the sequence times taken for trips 1, 2, 3, etc. Write an explicit formula for this sequence.
  3. Write the first five terms of the sequence of how much time it takes the drib to travel 1 mile, 2 miles, 3 miles, etc. Write an explicit formula for this sequence.
  4. Where is the drib 12 minutes after the first trip begins?
5. The Snowflake Curve.
Koch’s snowflake is a geometric figure built recursively, as follows. Stage 1 is an equilateral triangle whose sides are 1 unit in length. To produce Stage \(n\) from Stage \(n-1\text{,}\) perform the replacement of edges illustrated in Figure 1.5.1.
Figure 1.5.1. Each edge at stage \(n-1\) is replaced by four edges at stage \(n\)
The snowflake is the figure obtained after infinitely many stages. Stages 1, 2, 3 and the finished snowflake are shown in Figure 1.5.2.
Figure 1.5.2. The first three stages and the finished snowflake (https://commons.wikimedia.org/wiki/File:KochFlake.png)
  1. Write the first 5 terms of the sequence of the number of edges in Stages 1, 2, 3, etc. Write an explicit formula for this sequence.
  2. Write the first 5 terms of the sequence of the lengths of each edge in Stages 1, 2, 3, etc. Write an explicit formula for this sequence.
  3. Write the first 5 terms of the sequence of the total perimeter of the figure for Stages 1, 2, 3, etc. Write an explicit formula for this sequence. Hint: Multiply your results from the previous two parts.
  4. Write the first 5 terms of the sequence of the number of new equilateral triangle "bumps" added at Stages 1, 2, 3, etc. Write an explicit formula for this sequence. Hint: Adapt your result from part (a).
  5. Write the first 5 terms of the sequence of areas of each new equilateral triangle "bump" added at Stages 1, 2, 3, etc. Write an explicit formula for this sequence. Hint: The area of an equilateral triangle whose side measures \(s\) units of length is \(s^2\sqrt{3}/4\text{.}\) Hint: Use part (b).
  6. Write the first 5 terms of the sequence of the new area added (total area of all the new "bumps") at Stages 1, 2, 3, etc. Write an explicit formula for this sequence. Hint: Multiply your results from the previous two parts.
  7. Write the first 5 terms of the sequence of total area for Stages 1, 2, 3, etc. Write an explicit formula for this sequence. Hint: Sum the terms of the geometric sequence from the previous part. Watch out! The first couple of terms may not fit the pattern of the sequence.
  8. What is the perimeter of the snowflake?
  9. What is the area of the snowflake?

Subsection 1.5.2 Rational and Irrational Numbers

A rational number is a number that can be written in the form \(a/b\) for some integers \(a,b\text{.}\) An irrational number is a real number that is not rational. The standard symbol for the set of rational numbers is \(\Q\). In set notation, we have
\begin{equation*} \Q=\left\{\frac{a}{b}\colon a,b\in \Z, b\neq 0\right\}. \end{equation*}
The following is a classic proof by contradiction that proves that at least one irrational number exists.

Proof.

Suppose on the contrary that \(\sqrt{2}=a/b\) is rational, where \(a,b\) are integers. We may assume both \(a,b\) are positive, and we may assume that the fraction \(a/b\) is reduced, that is, that \(a,b\) have no common factors other than 1. Squaring both sides of \(\sqrt{2}=a/b\) and rearranging, we have \(2b^2=a^2\text{.}\) This says that \(a^2\) is even, so it must be that \(a\) itself is even. That means we can write \(a=2k\) for some integer \(k\text{.}\) Substituting \(2k\) for \(a\) in the equation \(2b^2=a^2\text{,}\) we get \(2b^2=(2k)^2=4k^2\text{,}\) which simplifies to \(b^2=2k^2\text{.}\) Now we see that \(b^2\) is even, so it must be that \(b\) is even. But this means that \(a,b\) are both divisible by 2, which contradicts the assumption that \(a,b\) share no common factors. We conclude that \(\sqrt{2}\) is irrational.

Checkpoint 1.5.4.

Justify the statement in the proof above that says "so \(a\) itself must be even". How would you convince your intelligent young cousin that "an odd times an odd must be odd"?
It turns out that irrational numbers are not rare or isolated among the real numbers; the rational numbers and irrational numbers are "everywhere" in the real line. The following proposition makes this statement precise. Recall that an open interval of the real line is a set of the form
\begin{equation*} (a,b)=\{x\in \R\colon a\lt x\lt b\} \end{equation*}
for some real numbers \(a,b\) with \(a\lt b\text{.}\) We say that a subset \(X\subseteq \R\) is dense in \(\R\) if every open interval contains an element of \(X\text{.}\)

Proof.

(This is an outline of the main points of the proof that \(\Q\) is dense in \(\R\text{.}\) In exercises below, you will complete the the details of the proof of the density of the rationals, and you will also prove the density of the irrationals.) Let \(a,b\) be given, with \(a\lt b\text{,}\) and let \(\epsilon=b-a\text{.}\) Choose an integer \(n\) large enough so that \(1/n \lt \epsilon\text{.}\) We claim that there is some integer multiple of \(1/n\) that lies between \(a\) and \(b\text{,}\) that is, there is some integer \(m\) such that \(a\lt m/n \lt b\text{.}\) If not, then there exist consecutive integer multiples \(k/n,(k+1)/n\) of \(1/n\) so that
\begin{equation*} k/n \leq a \lt b\leq (k+1)/n. \end{equation*}
But then we would have \(b-a\leq (k+1)/n -k/n = 1/n\text{,}\) a contradiction. Thus we have shown that the open interval \((a,b)\) contains a rational number. We conclude that \(\Q\) is dense in \(\R\text{.}\)

Checkpoint 1.5.6.

  1. In the proof outline of Proposition 1.5.5 above, how do we know that we can "choose an integer \(n\) large enough"?
  2. Explain why it is that "then we would have \(b-a\leq 1/n\text{.}\)
  3. What does that contradict?
  4. What allows us to "conclude that \(\Q\) is dense in \(\R\)"?

Exercises Exercises

1.
Let \(n\) be a positive integer. Show that either \(n\) is a perfect square (that is, \(n=k^2\) for some integer \(k\)), or \(\sqrt{n}\) is irrational.
Hint.
Let \(n\) be a positive integer, and suppose that \(\sqrt{n}=a/b\) is rational, where \(a,b\) are positive integers that share no common factors other than 1. Squaring and rearranging, we have \(nb^2=a^2\text{.}\) Let \(p\) be a prime factor of \(b\text{.}\) Explain why it must be that \(p|a\text{.}\) Explain why this implies that \(b=1\text{.}\) Explain how this implies the desired conclusion.
2.
Complete the proof of Proposition 1.5.5 by showing that the irrationals are dense in the reals.
3.
Choose an angle \(\theta_0\text{.}\) Starting at the point \((1,0)\text{,}\) walk around the unit circle in a counterclockwise direction, taking steps of size \(\theta_0\text{.}\) What is the smallest whole number of steps you have to take until you come for the first time to a point that you’ve already stepped on? Where is this first repeated location?
  1. Find the answer for \(\theta_0 = 20\) degrees.
  2. Find the answer for \(\theta_0 = 27\) degrees.
  3. Find the answer for \(\theta_0 = \sqrt{2}\) degrees.
  4. Find the answer for \(\theta_0 = 3\pi/2\) radians.
  5. Find the answer for \(\theta_0 = 1\) radian. You may use the fact that \(\pi\) is irrational.
  6. Find the answer for an arbitrary value of \(\theta_0\text{.}\) Suggestion: Rather than degrees or radians, you might consider using revolutions for your angle units.
4.
Your intelligent younger cousin declares to you that \(1.\overline{9}=1.999\ldots \text{(infinitely repeating 9's)}\) is less than 2. How do you explain that \(1.\overline{9}\) is actually equal to 2?
5.
Show that a number is rational if and only if it has a decimal representation that eventually repeats or terminates.
6.
Prove the following facts about terminating decimal expansions.
  1. Suppose that \(m=2^s5^t\) for some nonnegative integers \(s,t\text{.}\) Show that the rational number \(n/m\) (\(n\) also an integer) has a terminating decimal expansion.
  2. Suppose that the reduced rational number \(n/m\) (\(n,m\) integers with no common factors, \(m\neq 0\)) has a terminating decimal expansion. Show that \(m=2^s5^t\) for some nonnegative integers \(s,t\text{.}\)

Subsection 1.5.3 More Sets and Functions

Exercises Exercises

1.
Given a set \(A\text{,}\) the power set of \(A\text{,}\) denoted \({\mathcal P}(A)\), is defined to be the set of all subsets of \(A\text{.}\) For example, for \(A=\{a,b,c\}\text{,}\) we have
\begin{equation*} {\mathcal P}(A) = \{\emptyset,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}. \end{equation*}
  1. Why is the empty set considered a subset of \(A\text{?}\)
  2. Write out all of the possible functions from \(A\) to \(\{0,1\}\text{.}\) Hint: there are 8 in all.
  3. Can you see a natural one-to-one correspondence between the power set of \(A\) and the list of functions you just wrote down?
2.
Let \(S\) be a set. An algebra of subsets of \(S\) is a subset \({\mathcal A}\subseteq {\mathcal P}(S)\) of the power set of \(S\) (see Exercise 1.5.3.1 above) for which the following properties hold.
  1. \(\displaystyle \emptyset \in {\mathcal A}\)
  2. For every \(X,Y\in {\mathcal A}\text{,}\) \(X\cap Y\in {\mathcal A}\)
  3. For every \(X,Y\in {\mathcal A}\text{,}\) \(X\cup Y\in {\mathcal A}\)
  4. For every \(X\in {\mathcal A}\text{,}\) \(S\setminus X \in {\mathcal A}\)
  1. Show that the power set \({\mathcal P}(S)\) is an algebra of sets for any set \(S\text{.}\)
  2. Given an example of a collection of sets of some set \(S\) for which exactly three of the four set algebra properties hold.
3.
Let \(S\) be a set. Given a subset \(A\) of \(S\text{,}\) the characteristic function for \(A\) (relative to \(S\)), denoted \(\chi_A\colon S\to \{0,1\}\), is given by
\begin{equation*} \chi_A(x) =\left\{ \begin{array}{cc} 1 \amp \mbox{if } x\in A\\ 0 \amp \mbox{if } x\not\in A\\ \end{array}\right.. \end{equation*}
Let \(A,B\) be subsets of \(S\text{.}\) Prove the following. The symbol "\(\oplus\)" denotes addition modulo 2.
  1. \(A=B\) if and only if \(\chi_A=\chi_B\)
  2. \(\displaystyle (\chi_A)^2 = \chi_A\)
  3. \(\displaystyle \chi_{A\cap B} = \chi_A\cdot \chi_B\)
  4. \(\displaystyle \chi_{A\cup B} = \chi_A \oplus \chi_B \oplus (\chi_A\cdot \chi_B)\)
  5. \(\displaystyle \chi_{S\setminus A} = 1\oplus \chi_A\)
  6. \(\displaystyle \chi_{S\setminus (A\cup B)} = (1 \oplus \chi_A)(1 \oplus \chi_B)\)
4.
Let \(A,B,C\) be sets. Prove the following (the first two are distributive laws for sets and the second two are De Morgan’s laws). Hint: use characteristic functions from Exercise 1.5.3.3 above.
  1. \(\displaystyle A\cap(B\cup C)=(A\cap B)\cup (A\cap C)\)
  2. \(\displaystyle A\cup(B\cap C)=(A\cup B)\cap (A\cup C)\)
  3. \(\displaystyle S\setminus{(A\cap B)} = (S\setminus A) \cup (S\setminus B)\)
  4. \(\displaystyle S\setminus{(A\cup B)} = (S\setminus A) \cap (S\setminus B)\)
5.
A partition of a set \(S\) is a collection of nonempty subsets of \(S\) whose union is all of \(S\) and any two of which have empty intersection.
  1. Let \(S=\{a,b,c\}\text{.}\) Write out all possible partitions of \(S\text{.}\)
  2. Give an example of a collection of subsets of \(S=\{a,b,c\}\) whose union is all of \(S\text{,}\) but some two of which have nonempty intersection.
  3. Give an example of a collection of subsets of \(S=\{a,b,c\}\text{,}\) any two of which have empty intersection, but whose union is not all of \(S\text{.}\)
6.
An equivalence relation on a set \(S\) is a set \(E\subseteq S\times S\) of ordered pairs of elements of \(S\) that satisfies the following.
  1. \((x,x)\in E\) for every \(x\in S\) (the reflexive property)
  2. if \((x,y)\) is in \(E\) then \((y,x)\) is in \(E\) (the symmetric property)
  3. if \((x,y)\) is in \(E\) and \((y,z)\) is in \(E\text{,}\) then \((x,z)\) is in \(E\) (the transitive property)
  1. Write out all possible equivalence relations for \(S=\{a,b,c\}\text{.}\)
  2. Give an example of a set \(F\subseteq S\times S\) of ordered pairs of \(S=\{a,b,c\}\) that satisfies exactly two of the three properties in the definition of equivalence relation.

Subsection 1.5.4 Pythagorean Triples

A 3-tuple \((a,b,c)\) of positive integers is called a Pythagorean triple if there exists a right triangle with leg lengths \(a,b\) and hypotenuse length \(c\text{.}\) A Pythagorean triple is primitive if \(a,b,c\) have no common divisors (other than 1).
A point \((p,q)\) on the unit circle is called a rational point if both \(p,q\) are rational numbers. Let \(Q\) be the open first quadrant of the unit circle in the \(x,y\)-plane (that is, points on the unit circle with both coordinates positive). The following exercises explore the details of the one-to-one correspondences
\begin{equation*} \{\text{primitive Pythagorean triples}\} \longleftrightarrow \{\text{rational points on } Q\} \longleftrightarrow \{\text{rational numbers } a\gt 1\}. \end{equation*}
Figure 1.5.7. Pythagorean triple \((a,b,c)\) and associated unit circle point \((a/c,b/c)\)

Exercises Exercises

1.
Given a Pythagorean triple \((a,b,c)\) (not necessarily primitive), show that \((a/c,b/c)\) is a rational point on \(Q\) (see Figure 1.5.7).
2.
Let \((a,b,c)\) be a primitive Pythagorean triple. Show that \(a,c\) share no common divisors other than 1.
3.
Let \((p,q)\) be a point in \(Q\) with both \(p,q\) rational. Show that there is a unique reduced Pythagorean triple that maps to \((p,q)\) via \((a,b,c)\to (a/c,b/c)\text{.}\) Use this to explain why there is a one-to-one correspondence
\begin{equation*} \{\text{primitive Pythagorean triples}\} \longleftrightarrow \{\mbox{rational points on } Q\}. \end{equation*}
4.
Given a point \(P=(x,y)\) on \(Q\text{,}\) let \(L\) be the line through \(P\) and \((0,1)\text{.}\) Let \(s(P)\) be the \(x\)-coordinate of the intersection of \(L\) with the \(x\) axis. See Figure 1.5.8. This defines a one-to-one correspondence \(s\colon Q\to (1,\infty)\) called stereographic projection. Show that \(s\) is given by \(s(x,y) = \frac{x}{1-y}\text{.}\)
Figure 1.5.8. Stereographic projection
5.
Find a formula for \(s^{-1}\colon (1,\infty)\to Q\text{.}\) Verify that your formula really gives an inverse for \(s\) by showing that \(s^{-1}\of s=\One_{Q}\) and \(s\of s^{-1}=\One_{(1,\infty)}\text{.}\)
6.
Use the formulas for \(s,s^{-1}\) to explain why there is a one-to-one correspondence
\begin{equation*} \{\mbox{rational points on } Q\} \longleftrightarrow \{\text{rational numbers } a\gt 1\}. \end{equation*}
7.
From the correspondences established in this exercise, what is the rational number associated to the Pythagorean triple \((4,3,5)\text{?}\) To \((5,12,13)\text{?}\) What primitive Pythagorean triple corresponds to the rational number 3? To the rational number \(7/4\text{?}\)
PrevTopNext