Skip to main content
Logo image

Introduction to Groups and Geometries

David W. Lyons

Section 3.2 Möbius geometry

Möbius geometry provides a unifying framework for studying planar geometries. In particular, the transformation groups of hyperbolic and elliptic geometries in the sections that follow are subgroups of the group of Möbius transformations.

Subsection 3.2.1 Möbius transformations

A Möbius transformation (also called a linear fractional transformation) of the extended complex plane \(\extC\) is a function of the form
\begin{equation} f(z)= \frac{az+b}{cz+d}\tag{3.2.1} \end{equation}
where \(z\) is a complex variable, \(a,b,c,d\) are complex constants, and \(ad-bc\neq 0\text{.}\) To complete the definition, we make the assignments \(f(-d/c)=\infty\) and \(f(\infty)=a/c\) if \(c\neq 0\text{.}\) If \(c=0\text{,}\) we assign \(f(\infty)=\infty\text{.}\)
Note on notational convention: It is customary to use capital letters such as \(S,T,U\) to denote Möbius transformations. It is also customary to omit the parentheses, and to write \(Tz\) instead of \(T(z)\) to denote the value of a Möbius transformation.
Let \(f(x)=(ax+b)/(cx+d)\) be a function of a real variable \(x\) with real constants \(a,b,c,d\) with \(ad-bc\neq 0\) and \(c\neq 0\text{.}\)
  1. Show that \(\displaystyle \lim_{x\to -d/c}|f(x)|=\infty\text{.}\)
  2. Show that \(\displaystyle \lim_{x\to \infty}f(x)=a/c\text{.}\)

Instructor’s solution for Checkpoint 3.2.1.

  1. We have \(a(-d/c)+b = -\frac{ad-bc}{c}\neq 0\) (by assumption), so \(ax+b\to -\frac{ad-bc}{c}\neq 0\) and \(cx+d \to 0\) as \(x\to -d/c\text{,}\) so \(|f(x)|\to \infty\) as \(x\to -d/c\text{.}\)
  2. We have
    \begin{equation*} \frac{ax+b}{cx+d}=\frac{a}{c}\left(\frac{1+\frac{b}{ax}}{1+\frac{d}{cx}}\right). \end{equation*}
    It is clear that the latter expression tends to \(a/c\) as \(x\to \infty\text{.}\)
Show that the condition \(ad-bc\neq 0\) is necessary and sufficient for invertibility. Find a formula for the inverse of \(z\to (az+b)/(cz+d)\text{.}\)

Instructor’s solution for Checkpoint 3.2.2.

First, we solve \(w=\frac{az+b}{cz+d}\) for \(z\text{.}\) This yields \(z=\frac{dw-b}{-cw+a}\text{.}\) When we check the composition, we see that
\begin{align*} \frac{a\left(\frac{dw-b}{-cw+a}\right)+b}{c\left(\frac{dw-b}{-cw+a}\right)+d} \amp = \frac{a(dw-b)+b(-cw+a)}{c(dw-b)+d(-cw+a)}\\ \amp = w\frac{ad-bc}{ad-bc}. \end{align*}
Thus it is clear that the condition \(ad-bc\) is necessary and sufficient for invertibility.
Show that the composition of two Möbius transformations is a Möbius transformation. Suggestion: First show that the composition has the form \(z\to \frac{rz+s}{tz+u}\text{.}\) Next, instead of a brute force calculation to check that \(ru-ts\neq 0\text{,}\) use Checkpoint 3.2.2.

Instructor’s solution for Checkpoint 3.2.3.

Let \(Tz=\frac{az+b}{cz+d}\) and \(Sz=\frac{ez+f}{gz+h}\text{.}\) Then we have
\begin{align*} S(Tz)\amp = \frac{e\frac{az+b}{cz+d} +f}{g\frac{az+b}{cz+d}+h}\\ \amp = \frac{e(az+b)+f(cz+d)}{g(az+b)+h(cz+d)}\\ \amp = \frac{(ea+fc)z + (eb+fd)}{(ga+hc)z+(gb+hd)}\\ \amp = \frac{rz+s}{tz+u} \end{align*}
for \(r=ea+fc\text{,}\) \(s=eb+fd\text{,}\) \(t=ga+hc\text{,}\) \(u=gb+hd\text{.}\) The composition is invertible because both of its factors are invertible. It follows from the previous exercise that \(ru-ts\neq 0\text{.}\)

Definition 3.2.4.

The set of all Möbius transformations forms a group \(\M\text{,}\) called the Möbius group , under the operation of function composition. Möbius geometry is the pair \((\extC,\M)\text{.}\)
There is a natural relationship between Möbius group operations and matrix group operations. The map \({\mathcal T}\colon GL(2,\C)\to \M\) given by
\begin{equation} \left[ \begin{array}{cc}a\amp b\\ c\amp d\end{array}\right]\to \left[z\to \frac{az+b}{cz+d}\right]\tag{3.2.2} \end{equation}
is a group homomorphism. The kernel of \({\mathcal T}\) is the group of nonzero scalar matrices.
\begin{equation*} \ker{\mathcal T}=\left\{\left[ \begin{array}{cc}k\amp 0\\ 0\amp k\end{array}\right], k\neq 0\right\}\text{.} \end{equation*}
The quotient group \(GL(2,\C)/\ker{\mathcal T}\) is called the projective linear group \(PGL(2,\C)\text{.}\) Thus we have a group isomorphism
\begin{equation*} PGL(2,\C)\approx \M\text{.} \end{equation*}
Show that the map \({\mathcal T}\) is a group homomorphism. Show that the kernel of \({\mathcal T}\) is
\begin{equation*} \ker{\mathcal T}=\left\{\left[ \begin{array}{cc}k\amp 0\\ 0\amp k\end{array}\right], k\neq 0\right\}\text{.} \end{equation*}

Instructor’s solution for Checkpoint 3.2.5.

Using the same letters as in the solution to Checkpoint 3.2.3, the computation
\begin{equation*} \twotwo{e}{f}{g}{h}\twotwo{a}{b}{c}{c}=\twotwo{r}{s}{t}{u} \end{equation*}
verifies that \({\mathcal T}\) is a homomorphism. It is clear that the scalar matrices are contained in \(\ker{\mathcal T}\text{.}\) To see that \(\ker{\mathcal T}\) is contained in the scalar matrices, observe the Möbius transformation \(\left[z\to \frac{az+b}{cz+d}\right]\) is the identity if and only if \(a=d\neq 0\) and \(b=c=0\text{.}\)
Homotheties, rotations, translations, and inversions (see Table 3.1.4 in Section 3.1) are special cases of Möbius transformations. These basic transformations can be viewed as building blocks for general Möbius transformations, as follows.
  1. Identify the values of the coefficients \(a,b,c,d\) in a Möbius transformation \(z\to \frac{az+b}{cz+d}\) that is a homothety, rotation, translation, and inversion, respectively.
  2. Write a Möbius transformation that does "clockwise rotation by one-quarter rotation about the point \(2-i\)".

Instructor’s solution for Checkpoint 3.2.7.

    • A homothety must have \(b=c=0\) and \(a/d\gt 0\text{.}\)
    • A rotation must have \(b=c=0\) and \(|a|=|d|\text{.}\)
    • A translation must have \(c=0\text{,}\) \(b\neq 0\text{,}\) and \(a=d\neq 0\text{.}\)
    • An inversion must have \(a=d=0\) and \(c=b\neq 0\text{.}\)
  2. \(\displaystyle z \to e^{-i\pi/2}(z-(2-i)) + 2-i\)

Subsection 3.2.2 The Fundamental Theorem of Möbius Geometry

The Fundamental Theorem of Möbius Geometry says that all three-point sets are congruent. It will turn out to be convenient to work with the "standard" three-point set \(\{1,0,\infty\}\text{.}\) Given any three distinct complex numbers \(z_1,z_2,z_3\) it is easy to check that the transformation \(T\) given by
\begin{equation} Tz=\frac{z-z_2}{z-z_3}\frac{z_1-z_3}{z_1-z_2}\tag{3.2.3} \end{equation}
satisfies \(Tz_1=1,Tz_2=0,Tz_3=\infty\text{.}\)
Verify that (3.2.3) satisfies \(Tz_1=1,Tz_2=0,Tz_3=\infty\text{.}\)
It is easy to adapt (3.2.3) to the extended complex plane, where one of the \(z_i\) may be the point at infinity.
Prove Lemma 3.2.11 by finding explicit formulas for \(T\) for each of the three cases \(z_1=\infty\text{,}\) \(z_2=\infty\) and \(z_3=\infty\text{.}\)
Answer.
\begin{align*} (z_1=\infty) \amp \hspace{.2in}\amp Tz= \frac{z-z_2}{z-z_3}\\ (z_2=\infty) \amp \amp Tz= \frac{z_1-z_3}{z-z_3}\\ (z_3=\infty) \amp \amp Tz= \frac{z-z_2}{z_1-z_2} \end{align*}
The next Lemma lays lays the groundwork for proving the uniqueness of congruences between three-point sets.
Hint.
Solve \(z=\frac{az+b}{cz+d}\text{.}\) You will need to consider cases.

Instructor’s solution for Checkpoint 3.2.14.

Solving \(z=\frac{az+b}{cz+d}\text{,}\) we have \(cz^2+z(d-a)-b=0\text{.}\) If \(c\neq 0\text{,}\) we have 1 or 2 solutions
\begin{equation*} z=\frac{a-d\pm\sqrt{(d-a)^2+4bc}}{2c}. \end{equation*}
If \(c=0\) and \(d\neq a\text{,}\) we have two fixed points, \(z=b/(d-a),\infty\text{.}\) If \(c=0\text{,}\) \(d=a\text{,}\) and \(b\neq 0\text{,}\) then \(\infty\) is the only fixed point. Finally, if \(c=0\text{,}\) \(d=a\text{,}\) and \(b=0\text{,}\) then \(Tz=z\text{.}\)

Subsection 3.2.3 Cross ratio

Given three distinct points \(z_1,z_2,z_3\) in \(\extC\text{,}\) we write \((\cdot,z_1,z_2,z_3)\) to denote the unique Möbius transformation that satisfies \(z_1\to 1\text{,}\) \(z_2\to 0\text{,}\) and \(z_3\to \infty\) (the existence and uniqueness of this transformation is guaranteed by the Fundamental Theorem of Möbius Geometry). We write \((z_0,z_1,z_2,z_3)\) to denote the image of \(z_0\) under \((\cdot,z_1,z_2,z_3)\text{.}\) The expression \((z_0,z_1,z_2,z_3)\) is called the cross ratio of the 4-tuple \(z_0,z_1,z_2,z_3\text{.}\) By (3.2.3), we have the following explicit formula for the cross ratio.
\begin{equation} (z_0,z_1,z_2,z_3) = \frac{z_0-z_2}{z_0-z_3}\frac{z_1-z_3}{z_1-z_2}\tag{3.2.4} \end{equation}
The cross ratio is a useful tool because it is invariant under Möbius transformations. Here is the formal statement with a proof.
The transformations \((\cdot,z_1,z_2,z_3)\) and \((\cdot,Tz_1,Tz_2,Tz_3)\circ T\) both send \(z_1\to 1\text{,}\) \(z_2\to 0\text{,}\) and \(z_3\to \infty\text{,}\) so they must be equal, by the Fundamental Theorem. Now apply both transformations to \(z_0\text{.}\)

Subsection 3.2.4 Clines (generalized circles)

A Euclidean circle or straight line is called a cline (pronounced "kline") or generalized circle. The propositions and corollaries above show that the set of all clines is a single congruence class of figures in Möbius geometry.

Instructor’s solution for Checkpoint 3.2.19.

Suppose \((z_0,z_1,z_2,z_3)\) is real. Let \(T=(\cdot,z_1,z_2,z_3)\text{,}\) so that \(z_0\in T^{-1}(\extR)\text{.}\) Applying Proposition 3.2.17, we conclude that \(z_0\) lies on the unique cline through \(z_1,z_2,z_3\text{.}\) Conversely, suppose that \(z_0,z_1,z_2,z_3\) lie on a cline \(C\text{.}\) Again, let \(T=(\cdot,z_1,z_2,z_3)\text{.}\) By Proposition 3.2.17, we have \(C=T^{-1}(\extR)\text{,}\) so it must be that \(Tz_0=(z_0,z_1,z_2,z_3)\) is real.
Explain how Corollary 3.2.20 follows from Proposition 3.2.17.
Hint.
Let \(z_1,z_2,z_3\) be three points on \(C\) and let \(w_1=Tz_1,w_2=Tz_2,w_3=Tz_3\text{.}\) Let \(U=(\cdot,z_1,z_2,z_3)\) and let \(V=(\cdot,w_1,w_2,w_3)\text{.}\) Explain why \(T=V^{-1}U\) and hence that \(T(C)=V^{-1}U(C)=V^{-1}(\extR)\) must be a cline.

Instructor’s solution for Checkpoint 3.2.21.

Transformations \(T\) and \(V^{-1}U\) agree on three points \(z_1,z_2,z_3\text{,}\) so must be equal by the Fundamental Theorem of Möbius Geometry.
Explain how Corollary 3.2.22 follows from Proposition 3.2.17.
Hint.
Start here: Let \(C,D\) be two clines. Let \(z_1,z_2,z_3\) be three points on \(C\) and let \(w_1,w_2,w_3\) be three points on \(D\text{.}\) Let \(U=(\cdot,z_1,z_2,z_3)\) and let \(V=(\cdot,w_1,w_2,w_3)\text{,}\) and let \(T=V^{-1}U\text{.}\) Explain why \(T\) takes \(C\) to \(D\text{.}\)

Instructor’s solution for Checkpoint 3.2.21.

By Proposition 3.2.17, we have \(C=U^{-1}(\extR)\) and \(D=V^{-1}(\extR)\text{.}\) It follows that \(D=V^{-1}(U(C))=T(C)\text{.}\)

Subsection 3.2.5 Symmetry with respect to a cline

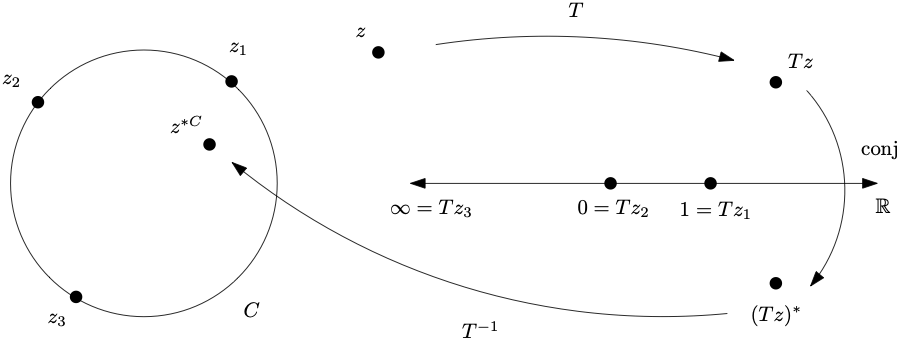
Geometrically, the conjugation map \(z\to z^{\ast}\) in the complex plane is reflection across the real line. This "mirror" symmetry generalizes to symmetry with respect to any cline, as follows. Given a cline \(C\) that contains \(z_1,z_2,z_3\) in \(\extC\text{,}\) let \(T=(\cdot,z_1,z_2,z_3)\text{.}\) Given any point \(z\text{,}\) the symmetric point with respect to \(C\) is
\begin{equation} z^{\ast C}= (T^{-1}\circ \conj \circ T)(z)\tag{3.2.5} \end{equation}
where \(\conj\colon \extC\to \extC\) is the extension of the conjugation map to the extended complex plane that sends \(\infty\to \infty^\ast=\infty\text{.}\) The idea is to map \(C\) to the real line via \(T\text{,}\) then conjugate, then map the real line back to \(C\text{.}\) See Figure 3.2.24.
Figure 3.2.24. Symmetric points \(z,z^{\ast C}\) with respect to the circle \(C\)
Show that the symmetric point of a symmetric point is the point you started with. That is, show that \((z^{\ast C})^{\ast C}=z\text{.}\) This allows us to speak of "a pair of symmetric points" without ambiguity.
Hint.
\((T^{-1}\circ \conj \circ T)\circ (T^{-1}\circ \conj\circ T) = \Id\)
Let \(z_1,z_2,z_3\) be three points on \(C\text{,}\) so that \(Sz_1,Sz_2,Sz_3\) are three points on \(S(C)\text{.}\) Let \(T=(\cdot,z_1,z_2,z_3)\) and let \(U=(\cdot,Sz_1,Sz_2,Sz_3)\text{.}\) By invariance of the cross ratio, we have
\begin{equation*} (U\circ S)z=Tz\text{.} \end{equation*}
Thus we have
\begin{align*} (Sz)^{\ast S(C)} \amp = (U^{-1}\circ \conj\circ U)(Sz) \;\; \text{(by definition)}\\ \amp = (S\circ S^{-1}\circ U^{-1}\circ \conj\circ U\circ S)(z)\\ \amp = S (S^{-1}\circ U^{-1}\circ \conj\circ U\circ S)(z)\\ \amp = S(T^{-1}\circ \conj \circ T)(z)\\ \amp = S(z^{\ast C}) \end{align*}
as desired.

Subsection 3.2.6 Normal forms

We conclude this section on Möbius geometry with a discussion of the normal form of a Möbius transformation. We begin with a Lemma.
Now suppose that a Möbius transformation \(T\) has two fixed points, \(p\) and \(q\text{.}\) Let \(S\) be given by \(Sz = \frac{z-p}{z-q}\text{.}\) Let \(w=Sz\) and let \(U=S\circ T\circ S^{-1}\) be the transformation of the \(w\)-plane that is conjugate to \(T\) via \(S\) (see Exercise Group 1.3.3.3–6). It is easy to check that \(U\) has exactly two fixed points \(0\) and \(\infty\text{.}\) Applying the previous Lemma, we have \(Uw=\alpha w\) for some nonzero \(\alpha\in \C\text{.}\) Applying both sides of \(S\circ T=U\circ S\) to \(z\text{,}\) we have the following normal form for \(T\text{.}\)
\begin{equation} \frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}\tag{3.2.6} \end{equation}
The transformation \(T\) is called elliptic, hyperbolic, or loxodromic if \(U\) is a rotation (\(|\alpha|=1\)), a homothety (\(\alpha \gt 0\)), or neither, respectively.
Finally, suppose that a Möbius transformation \(T\) has exactly one fixed point at \(p\text{.}\) Let \(S\) be given by \(Sz = \frac{1}{z-p}\text{.}\) Again, let \(w=Sz\) and let \(U=S\circ T\circ S^{-1}\text{.}\) This time, \(U\) has exactly one fixed point at \(\infty\text{.}\) Applying the Lemma, we have \(Uw=w+\beta\) for some nonzero \(\beta\in \C\text{.}\) Applying both sides of \(S\circ T=U\circ S\) to \(z\text{,}\) we have the following normal form for \(T\text{.}\)
\begin{equation} \frac{1}{Tz-p}= \frac{1}{z-p}+\beta\tag{3.2.7} \end{equation}
A Möbius transformation of this type is called parabolic. Here is a summary of the classification terminology associated with normal forms.
Table 3.2.29. Summary of normal forms of \(T\in \M\)
normal form type normal form conjugate transformation type
elliptic \(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}, |\alpha|=1\) rotation
hyperbolic \(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}, \alpha\gt 0\) homothety
loxodromic \(\frac{Tz-p}{Tz-q}= \alpha \frac{z-p}{z-q}, \alpha\neq 0\) composition of homothety with rotation
\(|\alpha|\neq 1, \alpha\not\gt 0\)
parabolic \(\frac{1}{Tz-p}= \frac{1}{z-p} + \beta, \beta\neq 0\) translation

Subsection 3.2.7 Steiner circles

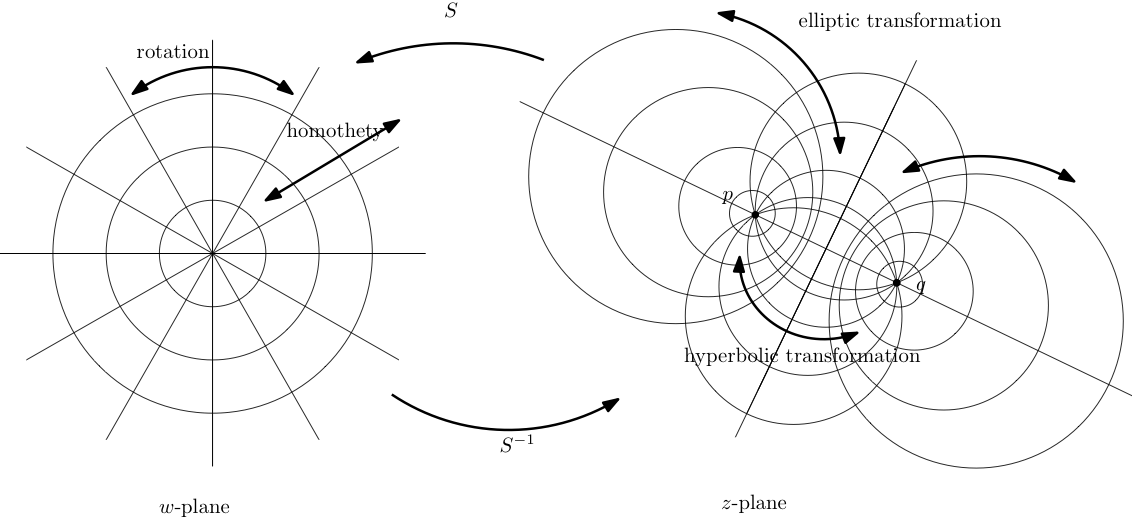
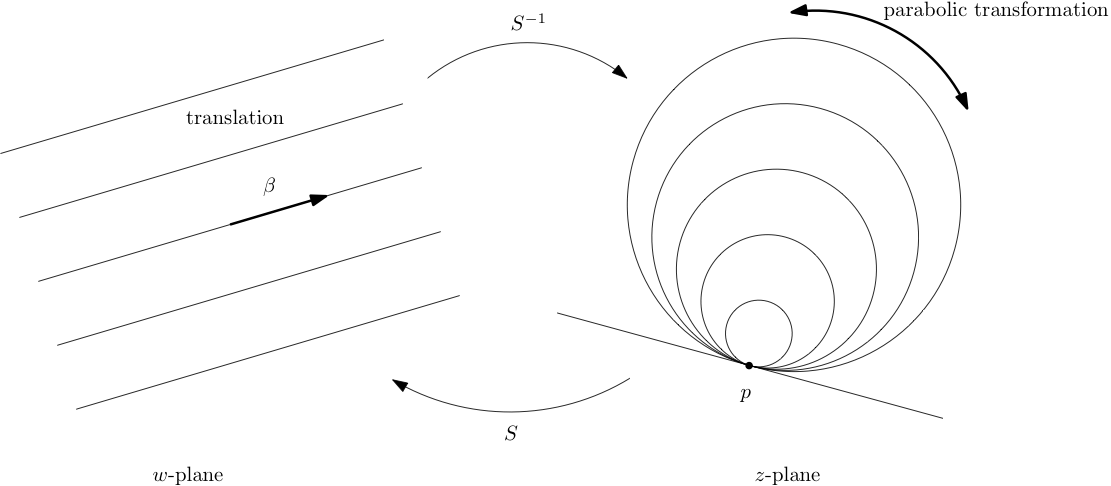
Figure 3.2.30. The polar coordinate grid and Steiner circle coordinate grid
Figure 3.2.31. Degenerate coordinate grid lines and degenerate Steiner circles
The discussion of normal forms show that any non-identity Möbius transformation is conjugate to one of two basic forms, \(w\to \alpha w\) or \(w\to w+\beta\text{.}\) The natural coordinate system for depicting the action of \(w\to \alpha w\) is standard polar coordinates. See Figure 3.2.30. A homothety is a flow along radial lines and a rotation is a flow around polar circles. The natural "degenerate" coordinate system for depicting a translation \(w\to w+\beta\) is a family of lines parallel to the line that contains the origin and \(\beta\text{.}\) A translation by \(\beta\) is a flow along these parallel lines. See Figure 3.2.31.
Pulling the polar and degenerate coordinate grids back to the \(z\)-plane by \(S^{-1}\) leads to coordinate grids called Steiner circles. 1  In the case where \(T\) has two fixed points \(p,q\text{,}\) the conjugating map \(Sz=\frac{z-p}{z-q}\) takes \(p\to 0\text{,}\) \(q\to \infty\text{.}\) Therefore \(S^{-1}\) maps \(0\to p\) and \(\infty \to q\text{.}\) The transformation \(S^{-1}\) maps radial lines in the \(w\)-plane to clines in the \(z\)-plane that contain \(p\) and \(q\) called Steiner circles of the first kind and \(S^{-1}\) maps polar circles in the \(w\)-plane to clines in the \(z\)-plane called Steiner circles of the second kind or circles of Apollonius. See Figure 3.2.30.
In the case where \(T\) has one fixed point \(p\text{,}\) the conjugating map \(Sz=\frac{1}{z-p}\) sends \(p\to \infty\text{,}\) so \(S^{-1}\) maps \(\infty \to p\text{,}\) and \(S^{-1}\) maps lines in the \(w\)-plane that are parallel to the line through \(0\) and \(\beta\) to clines in the \(z\)-plane that contain \(p\text{.}\) Every cline in this family is tangent to every other cline in this family at exactly the one point \(p\text{.}\) Clines in this family are called degenerate Steiner circles. See Figure 3.2.31. Table 3.2.32 summarizes the graphical depiction of Möbius transformations.
Table 3.2.32. Summary of Steiner circle pictures of Möbius transformations
normal form type graphical dynamic
elliptic flow along Steiner circles of the second kind
hyperbolic flow along Steiner circles of the first kind
loxodromic composition of elliptic and hyperbolic flows
parabolic flow along degenerate Steiner circles

Exercises 3.2.8 Exercises

Essential exercises: 1, 2, 3a, 4, 5, 6, 7
At least discuss the idea:
May be omitted: 3b, 8, 9

1. Decomposition of Möbius transformations into four basic types.

  1. Explain why a transformation of the form \(z\to az\text{,}\) with \(a\) any nonzero complex constant, is a composition of a homothety and a rotation.
  2. Explicitly identify each homothety, rotation, translation, and inversion in (3.2.8) to (3.2.11) in the derivation below for the case \(c\neq 0\text{.}\)
    \begin{align} z \amp \to cz+d\tag{3.2.8}\\ \amp\to \frac{1}{cz+d}\tag{3.2.9}\\ \amp\to \frac{bc-ad}{cz+d} + a\tag{3.2.10}\\ \amp\to \frac{1}{c}\left(\frac{bc-ad}{cz+d} + a\right)\tag{3.2.11}\\ \amp = \frac{az+b}{cz+d}\tag{3.2.12} \end{align}
  3. Write your own decomposition for the case \(c=0\text{.}\)

Instructor’s solution for Exercise 3.2.8.1.

  1. Use polar form \(a=|a|e^{i\arg a}\text{.}\)
    1. homothety and a rotation (multiplying by \(c\)), followed by translation (adding \(d\))
    2. inversion
    3. homothety and rotation (multiplying by \(bc-ad\)), followed by translation (adding \(a\))
    4. homothety and rotation (multiplying by \(1/c\))
  3. If \(c=0\text{,}\) then \(ad-bc=ad\neq 0\text{,}\) so \(d\neq 0\text{,}\) and we have
    \begin{equation*} z = \frac{az+b}{d} = \frac{a}{d}z+\frac{b}{d} \end{equation*}
    a homothety and rotation (multiplying by \(a/d\) followed by a translation (adding \(b/d\)).

2.

Prove the Fundamental Theorem of Möbius Geometry (Proposition 3.2.15).
Hint.
Start by using Lemma 3.2.11 to get a Möbius transformation \(U\) that maps \(z_1,z_2,z_3\) to \(1,0,\infty\text{,}\) and there is a Möbius transformation \(V\) that maps \(w_1,w_2,w_3\) to \(1,0,\infty\text{.}\)

Instructor’s solution for Exercise 3.2.8.2.

By Lemma 3.2.11, there exists a Möbius transformation \(U\) that maps \(z_1,z_2,z_3\) to \(1,0,\infty\text{,}\) and there is a Möbius transformation \(V\) that maps \(w_1,w_2,w_3\) to \(1,0,\infty\text{.}\) It is easy to see that \(T=V^{-1}U\) satisfies \(Tz_i=w_i\) for \(i=1,2,3\text{.}\) Now suppose that there is another Möbius transformation \(S\) such that \(Sz_i=w_i\) for \(i=1,2,3\text{.}\) It is easy to check that \(S\circ T^{-1}\) fixes the three points \(w_1,w_2,w_3\text{.}\) By Lemma 3.2.13, we have \(S\circ T^{-1}=\Id\text{,}\) so \(S=T\text{.}\)

3.

Find Möbius transformations that make the following assignments.
  1. \(\displaystyle 1\to a, 0\to b, \infty\to c\)
  2. \(\displaystyle a\to d, b\to e, c\to f\)

Instructor’s solution for Exercise 3.2.8.3.

  1. Start with the inverse of the desired transformation, then take the inverse using matrix methods.
    \begin{align*} [a\to 1, b\to 0,c\to \infty] \amp = \left[z\to \frac{z-b}{z-c}\frac{a-c}{a-b}\right]\\ \amp \leftrightarrow \twotwo{a-c}{b(c-a)}{a-b}{c(b-a)}\\ [a\to 1, b\to 0,c\to \infty]^{-1} \amp \leftrightarrow \twotwo{c(b-a)}{b(a-c)}{b-a}{a-c} \\ [1\to a, 0\to b,\infty\to c] \amp = \left[z\to \frac{c(b-a)z +b(a-c)}{(b-a)z+a-c} \right] \end{align*}
  2. Put together the pieces from the previous part.
    \begin{align*} [a\to 1, b\to 0,c\to \infty] \amp = \left[z\to \frac{z-b}{z-c}\frac{a-c}{a-b}\right]\\ [1\to d, 0\to e,\infty\to f] \amp = \left[z\to \frac{f(e-d)z +e(d-f)}{(e-d)z+d-f} \right]\\ [a\to d,b\to e,c\to f] \amp = [1\to d, 0\to e,\infty\to f]\circ [a\to 1, b\to 0,c\to \infty]\\ \amp \leftrightarrow \twotwo{f(e-d)}{e(d-f)}{e-d}{d-f}\twotwo{a-c}{b(c-a)}{a-b}{c(b-a)}\\ \amp \leftrightarrow \twotwo{ef(b-c)+df(c-a)+ed(a-b)}{abf(d-e)+bcd(e-f) +ace(f-d)}{d(c-b)+e(a-c)+f(b-a)}{ab(d-e)+bc(e-f)+ac(f-d)} \end{align*}

4.

Prove Proposition 3.2.17. Suggestion: Let \(Tz=\frac{az+b}{cz+d}\text{,}\) then manipulate \(Tz=(Tz)^\ast\) to an equation with \(|z|^2,z,z^\ast\) terms and coefficients involving \(a,b,c,d\) and their conjugates. For the case when the coefficient of \(|z|^2\) is not zero, use "complex completing the square" (see (1.1.24)) to derive the equation of a circle. Peek at the first part hint below if you need to, and use it to work partially forwards from \(Tz=(Tz)^\ast\text{,}\) and partially backwards from the equation in the hint. For the case when the coefficient of \(|z|^2\) is zero, derive the equation for a line. For the "furthermore" statement, you will need to show that any three points in the plane determine a unique circle or straight line. This is a Euclidean statement, and it is straightforward to prove this using Euclidean methods (peek at the second part of the hint below if you need to).
Hint.
Equation for the circle:
\begin{equation*} \left| z-\left(\frac{a^\ast d-bc^\ast}{ac^\ast -a^\ast c}\right)\right|^2 = \left|\frac{ad-bc}{ac^\ast -a^\ast c}\right|^2 \end{equation*}
Why three noncollinear points \(P,Q,R\) determine a unique circle? The center \(C\) of the circle must be the intersection of the perpendicular bisectors of segments \(PQ\text{,}\) \(QR\text{.}\) The radius must be the distance from \(C\) to any one of \(P,Q,R\text{.}\)

Instructor’s solution for Exercise 3.2.8.4 (proof of Proposition 3.2.17).

Starting with \(Tz=(Tz)^\ast\text{,}\) we get
\begin{equation*} |z|^2 (ac^\ast-a^\ast c) + z(ad^\ast -b^\ast c)+z^\ast(-a^\ast d+bc^\ast) = b^\ast d-bd^\ast. \end{equation*}
If \(ac^\ast -a^\ast c\neq 0\text{,}\) let \(\alpha=\frac{-b c^\ast +a^\ast d}{ac^\ast -a^\ast c}\text{,}\) then complete the square to get
\begin{equation*} |z-\alpha|^2 = \frac{b^\ast d -bd^\ast}{\alpha} + |\alpha|^2. \end{equation*}
Manipulate the right hand side to \(\left|\frac{ad-bc}{ac^\ast -a^\ast c}\right|^2\text{.}\) For the case \(ac^\ast -a^\ast c=0\text{,}\) let \(\gamma=ad^\ast -b^\ast c\) and \(\delta=bd^\ast\text{.}\) Then the equation
\begin{equation*} z(ad^\ast -b^\ast c)+z^\ast(-a^\ast d+bc^\ast) = b^\ast d-bd^\ast \end{equation*}
becomes \(\im(\gamma z+\delta)=0\text{,}\) which is the equation for a line.
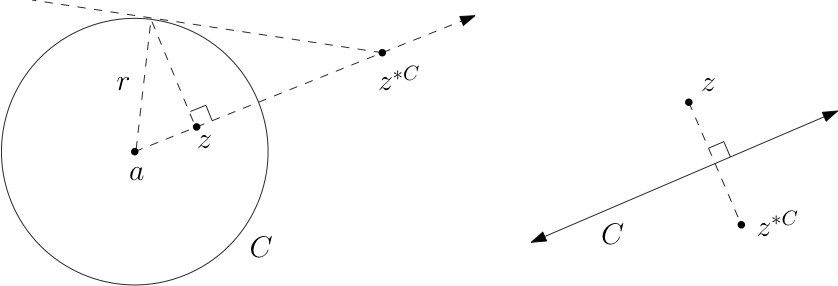
Figure 3.2.33. Geometry for symmetric points \(z,z^{\ast C}\) with respect to the cline \(C\)

5. Symmetry with respect to a cline.

  1. Prove Proposition 3.2.26 by completing the details in the following outline. Let \(C=T^{-1}(\extR)\) be a cline that contains points \(z_1,z_2,z_3\text{,}\) where \(T=(\cdot,z_1,z_2,z_3)\text{.}\) First, consider the case when \(C\) is a circle, say, with equation \(|z-a|=r\text{,}\) where \(a,r\) are the center and radius, respectively, of \(C\) (see (1.1.22)).
    1. Square both sides of \(|z-a|=r\) and solve for \(z^\ast\) to get
      \begin{equation*} z^\ast = \frac{r^2}{z-a}+a^\ast\text{.} \end{equation*}
    2. We have
      \begin{align*} (\conj\circ T)(z) \amp = (z^\ast,z_1^\ast,z_2^\ast,z_3^\ast)\\ \amp = \left(z^\ast, \frac{r^2}{z_1-a}+a^\ast,\frac{r^2}{z_2-a}+a^\ast,\frac{r^2}{z_3-a}+a^\ast\right)\\ \amp \stackrel{(1)}{=} \left(\frac{r^2}{z^\ast - a^\ast}+a,z_1,z_2,z_3\right)\\ \amp = T\left(\frac{r^2}{(z-a)^\ast}+a\right). \end{align*}
      Explain how invariance of the cross ratio is used to justify the equality (1) in this derivation.
    3. Explain how we can conclude that \(z^{\ast C}= \frac{r^2}{(z-a)^\ast}+a\text{,}\) and that indeed this does not depend on the choice of \(z_1,z_2,z_3\text{.}\)
    4. Now suppose that \(C\) is a line, say, with equation \(\im(az+b)=0\) (see (1.1.23)). This is the same as \(az+b=(az+b)^\ast\text{.}\) Solve to get
      \begin{equation*} z^\ast = \frac{az+b-b^\ast}{a^\ast}. \end{equation*}
    5. We have
      \begin{align*} (\conj\circ T)(z) \amp = (z^\ast,z_1^\ast,z_2^\ast,z_3^\ast)\\ \amp = \left(z^\ast,\frac{az_1+b-b^\ast}{a^\ast},\frac{az_2+b-b^\ast}{a^\ast}, \frac{az_3+b-b^\ast}{a^\ast}\right)\\ \amp \stackrel{(1)}{=} \left(\frac{z^\ast a^\ast + b^\ast - b}{a},z_1,z_2,z_3\right)\\ \amp = T\left(\frac{z^\ast a^\ast + b^\ast - b}{a}\right). \end{align*}
      Explain how invariance of the cross ratio is used to justify the equality (1) in this derivation.
    6. Explain how we can conclude that \(z^{\ast C}=\frac{z^\ast a^\ast + b^\ast - b}{a}\text{,}\) and that indeed this does not depend on the choice of \(z_1,z_2,z_3\text{.}\)
  2. Show that \(z,z'\) are symmetric with respect to a circle \(C\) with center \(a\) and radius \(r\) if and only if \(|z-a||z'-a|=r^2\) and \(z,z'\) lie on the same ray emanating from \(a\text{.}\) See Figure 3.2.33. Hint.
    The equation for \(z^{\ast C}\) in part iii gives \((z'-a)(z-a)^\ast = r^2\text{.}\) For the first statement, take the norm of both sides. For the second statement, take the argument of both sides.
  3. Show that \(z,z'\) are symmetric with respect to a line \(C\) if and only if \(z,z'\) are reflections of one another across \(C\text{.}\) See Figure 3.2.33.

Instructor’s solution for Exercise 3.2.8.5.

    1. Use \(|z-a|^2 = (z-a)(z-a)^\ast\text{.}\) Set the latter expression equal to \(r^2\) and solve for \(z^\ast\text{.}\)
    2. The second equality uses part i. Equality (1) uses invariance of the cross ratio, applying the Möbius transformation
      \begin{align*} u\amp \to u-a^\ast\\ \amp \to \frac{r^2}{u-a^\ast}\\ \amp \to \frac{r^2}{u-a^\ast}+a \end{align*}
      to all four entries in the cross ratio immediately preceding the equals sign labeled (1).
    3. Apply \(T^{-1}\) to the first and last expressions in the derivation.
    4. A complex number \(u\) is real if and only if \(u=u^\ast\text{.}\) Apply this to \(u=az+b\text{.}\) Solving for \(z^\ast\) is straightforward.
    5. This is similar to ii above. Equality (1) uses invariance of the cross ratio, applying the Möbius transformation
      \begin{align*} u\amp \to a^\ast u\\ \amp \to a^\ast u + b^\ast -b\\ \amp \to \frac{a^\ast u + b^\ast -b}{a} \end{align*}
      to all four entries in the cross ratio immediately preceding the equals sign labeled (1).
    6. Apply \(T^{-1}\) to the first and last expressions in the derivation.
  2. Rearranging the equation for \(z'=z^{\ast C}\) in part iii, we have \((z-a)(z'-a)=r^2\text{.}\) Taking the norm of both sides, we have \(|z-a||z'-a|=r^2\text{.}\) Taking the argument of both sides, we have \(\arg(z'-a)-\arg(z-a)=0\text{.}\) This implies that \(z,z'\) lie on the same ray emanating from \(a\text{.}\)
  3. Let \(C\) be a line, and let \(R,T\) be a rotation and a translation, respectively, such that \(RT(C) =\extR\text{.}\) Given a pair \(z,z'\) that are symmetric with respect to \(C\text{,}\) we have that \((RTz)^\ast = RT(z^\ast)\text{,}\) so that \(w=RTz,w'=RT(z^\ast)\) are reflections of one another across the real line. Since \(R,T\) are distance and angle preserving, we conclude that \(z=T^{-1}R^{-1}w,z'=T^{-1}R^{-1}(w')\) must be reflections of one another across the line \(C=T^{-1}R^{-1}(\extR)\text{.}\)

Normal forms and Steiner circles.

7.
Find the normal form and sketch a graph using Steiner circles for the following transformations.
  1. \(\displaystyle z\to \frac{1}{z}\)
  2. \(\displaystyle z\to \frac{3z-1}{z+1}\)
8.
Let \(p\) be the single fixed point of a Möbius transformation that is conjugate to \(w\to w+\beta\) via \(Sz=\frac{1}{z-p}\text{.}\) Show that the single line in the degenerate Steiner clines through \(p\) is parallel to the direction given by \(\beta^\ast\text{.}\)
Hint.
Show that \(S^{-1}w=\frac{pw+1}{w}\text{,}\) so \(S^{-1}\) takes \(0,\beta,\infty\) to \(\infty,\frac{p\beta+1}{\beta},p\text{.}\) Thus the single degenerate Steiner straight line through \(p\) is in the direction given by \(\frac{p\beta+1}{\beta}-p =\frac{1}{\beta}\propto \beta^\ast\text{.}\)
9.
Show that a (generalized) circle of Apollonius (a Steiner circle of the second kind) is characterized as the set of points of the form
\begin{equation*} C=\left\{P\in \C\colon \frac{d(P,A)}{d(P,B)}=k\right\} \end{equation*}
for some \(A,B\in \C\) and some real constant \(k\gt 0\text{.}\)

Instructor’s solution for Exercise 3.2.8.6 (proof of Lemma 3.2.28).

Let \(Tz=\frac{az+b}{cz+d}\text{.}\) Suppose that \(T\) fixes \(0,\infty\text{.}\) We have \(0=T(0)=b/d\text{,}\) so \(b=0\text{.}\) We have \(T\infty = a/c\text{,}\) so \(c=0\text{.}\) Setting \(\alpha = a/d\text{,}\) it must be that \(\alpha\neq 0\) (otherwise \(T\) would be constant) and \(\alpha\neq \infty\) (otherwise \(d=0\text{,}\) which violates the requirement \(ad-bc=0\)). Thus we have \(Tz=az/d = \alpha z\) for some \(\alpha\neq 0\text{.}\) Now suppose \(T\) has a single fixed point at \(\infty\text{.}\) Then \(T\infty = a/c\text{,}\) so \(c=0\text{.}\) Let \(\alpha=a/d,\beta=b/d\text{,}\) so that \(Tz=\alpha z +\beta\text{.}\) If \(\alpha\neq 1\text{,}\) then \(-\beta/\alpha\) is another fixed point, so it must be that \(\alpha=1\text{.}\) If \(\beta=0\text{,}\) then \(T\) is the identity, but that contradicts our assumption that \(T\) has a single fixed point. Thus \(Tz=z+\beta\) for some \(\beta\neq 0\text{.}\)

Instructor’s solution for Exercise 3.2.8.7.

  1. The fixed points of \(T\) are \(\pm 1\text{,}\) so the normal form is
    \begin{equation*} \frac{Tz-1}{Tz+1}=\alpha\frac{z-1}{z+1}. \end{equation*}
    Putting \(z=2\) and solving for \(\alpha\text{,}\) we get \(\alpha=-1\text{.}\) The Steiner circles of the first kind are circles through \(\pm 1\) (and the real axis), and Steiner circles of the second kind are orthogonal to the first family (including the imaginary axis).
  2. Solving \(Tz=z\text{,}\) we get \((z-1)^2=0\text{,}\) so \(T\) has a single (degenerate) fixed point at \(1\text{.}\) The normal form is
    \begin{equation*} \frac{1}{Tz-1} = \frac{1}{z-1}+\beta. \end{equation*}
    Putting \(z=0\) and solving for \(\beta\text{,}\) we get \(\beta=1/2\text{.}\) It is clear that \(T\) takes the real axis to itself, so degenerate Steiner circles are tangent to the real axis at \(1\text{.}\)

Instructor’s solution for Exercise 3.2.8.8.

We have
\begin{align*} S\amp \leftrightarrow \twotwo{0}{1}{1}{-p}\\ S^{-1}\amp \leftrightarrow \twotwo{-p}{-1}{-1}{0}\sim \twotwo{p}{1}{1}{0} \end{align*}
so \(S^{-1}w=\frac{pw+1}{w}\text{,}\) so \(S^{-1}\) takes \(0,\beta,\infty\) to \(\infty,\frac{p\beta+1}{\beta},p\text{.}\) Thus, \(S^{-1}\) transforms the line through \(0,\beta\) in the \(w\)-plane to the line through \(\frac{p\beta+1}{\beta},p\) in the \(z\)-plane. This degenerate Steiner line has a direction vector given by \(\frac{p\beta+1}{\beta}-p=\frac{p\beta+1-p\beta}{\beta} =\frac{1}{\beta} = \frac{\beta^\ast}{|\beta|^2}\propto \beta^\ast\text{,}\) as claimed.

Instructor’s solution for Exercise 3.2.8.9.

By definition, Steiner circles of the second kind are sets of the form \(S^{-1}(\{w\colon |w|=r\})\) for some \(w=Sz=\frac{z-p}{z-q}\) (some distinct \(p,q\in C)\text{.}\) Setting \(P=p\text{,}\) \(Q=q\text{,}\) \(k=r\text{,}\) we have
\begin{equation*} S^{-1}(\{|w|=r\}) = \left\{P\colon \frac{d(P,A)}{d(Q,B)}=k\right\}. \end{equation*}
The convention for which Steiner circles are considered "first" or "second" kinds is not universal. Here we follow the convention used by Ahlfors [1] and Henle [4].
PrevTopNext